Send
Close Add comments:
(status displays here)
Got it! This site "creationpie.org" uses cookies. You consent to this by clicking on "Got it!" or by continuing to use this website. Note: This appears on each machine/browser from which this site is accessed.
Mathematical constants and Hebrew pi
1. Mathematical constants and Hebrew pi
In mathematics, a constant is a name for a number that does not change.
The name π (Greek letter) or pi is 3.1415.,., the ratio of the circumference to the diameter of a circle.
The name e is the exponential constant 2.71828..., the number whose function derivative is itself (a fixed point).
... and so on ...
2. Mathematical constant pi
The Greek symbol
π, pronounced "
pie", is used to refer the ratio of the diameter
d of a circle to its circumference
c.
c = π * d = π d

The radius
r of a circle is half the diameter
d, so the following holds.
c = π * d = π*2*r = 2 π * r = 2 π r
Numbers such as
π are transcendental and, like irrational numbers, have no exact representation and can only be approximated.
3. Approximation
Leibniz (1646-1716) discovered the following infinite series that sums to
π/4.
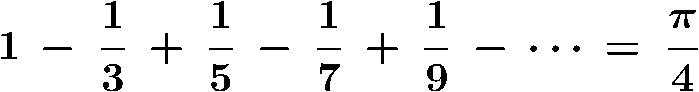
There are many other sequences that sum to
π (or a ratio involving
π).
The value of
π is the approximate value of
3.1415. A more precise value approximation is
3.1415926535898.
4. Rational approximation of π
Transcendental numbers can be approximated by a rational number as the ratio of two integers.
Consider the transcendental number
π and the approximation of
1 over
π which provides a ratio between
0.0 and
1.0. The smallest set of integers that gets close to
π, from a brute-force analysis, is
22/7.

5. Manual approach

A manual approach is to start trying values for numerator and denominator and see which is closest. There may be clever ways to prune the search. Here is a grid to show the best approximations for denominators ranging from
1 to
10 and numerators ranging from
0 to
10. The best approximation below and above the desired result is in light green while the others are in gray.
6. Program approach
With the use of computer programming code, is easy to find rational approximations to non-rational numbers. Note: The program is intended to be somewhat clear, but not necessarily the most efficient.
7. Lua code - one over pi
Here is the Lua code [#1]
8. Output - one over pi
The output shows the best
20 integer ratio approximations where the denominator ranges from
1 to
300.
0.31830988618379... (desired value is 1/pi)
Here is the output of the Lua code.
9. Old Testament value of pi
 1 Kings 7:23 … ten cubits from the one brim to the other: it was round all about… and a line of thirty cubits did compass it round about. [kjv]
1 Kings 7:23 … ten cubits from the one brim to the other: it was round all about… and a line of thirty cubits did compass it round about. [kjv]
 … וקוה … [he]
… וקוה … [he]
 2 Chronicles 4:2 … ten cubits from brim to brim, round in compass… and a line of thirty cubits did compass it round about. [kjv]
2 Chronicles 4:2 … ten cubits from brim to brim, round in compass… and a line of thirty cubits did compass it round about. [kjv]
 … וקו … [he]
… וקו … [he]
Many have used the above verse (same numbers) to argue that the Hebrews of the Old Testament, and therefore the sacred writings, did not have an understanding of the mathematical value of pi since it appears to be
3 and not
3.141516....
10. Old Testament value of pi
 1 Kings 7:23 … ten cubits from the one brim to the other: it was round all about… and a line of thirty cubits did compass it round about. [kjv]
1 Kings 7:23 … ten cubits from the one brim to the other: it was round all about… and a line of thirty cubits did compass it round about. [kjv]
 2 Chronicles 4:2 … ten cubits from brim to brim, round in compass… and a line of thirty cubits did compass it round about. [kjv]
2 Chronicles 4:2 … ten cubits from brim to brim, round in compass… and a line of thirty cubits did compass it round about. [kjv]
11. Gematria
12. 1 Kings 7:23
KJV: And he made a molten sea, ten cubits from the one brim to the other: it was round all about, and his height was five cubits: and a line of thirty cubits did compass it round about.
Hebrew: ויעש את הים מוצק עשר באמה משפתו עד שפתו עגל סביב וחמש באמה קומתו וקוה שלשים באמה יסב אתו סביב׃
Greek: και εποιησεν την θαλασσαν δεκα εν πηχει απο του χειλους αυτης εως του χειλους αυτης στρογγυλον κυκλω το αυτο πεντε εν πηχει το υψος αυτης και συνηγμενοι τρεις και τριακοντα εν πηχει εκυκλουν αυτην
13. 2 Chronicles 4:2
KJV: Also he made a molten sea of ten cubits from brim to brim, round in compass, and five cubits the height thereof; and a line of thirty cubits did compass it round about.
Hebrew: ויעש את הים מוצק עשר באמה משפתו אל שפתו עגול סביב וחמש באמה קומתו וקו שלשים באמה יסב אתו סביב׃
Greek: και εποιησεν την θαλασσαν χυτην πηχεων δεκα την διαμετρησιν στρογγυλην κυκλοθεν και πηχεων πεντε το υψος και το κυκλωμα πηχεων τριακοντα
14. Gerald Schroeder
There have been many attempts to explain this. One by Gerald Schroeder (from earlier work) is summarized as follows.
The gematria value of "line" in 1 Kings 7:23 is 111.
The gematria value of "line" in 2 Chronicles 4:2 106.
Multiplying 3 by the ratio of 111/106 = 0.95495495... ≈ 3.1416... (correct to four decimal places).
Summary:
The Hebrews wrote the passages.
The translation appears to have errors.
The implication is that the underlying text is not true.
A way was found to fix the translation.
It is not clear why one would use such an encoding to hide the actual value. In this respect, finding a way to fix the issue appears much like an
ELS (Equidistant Letter Sequence).
15. Converse error
Fixing a translation or the interpretation of the underlying text does not, in and of itself, make the underlying text true if that text has intended meaning outside of the text (e.g., a creator God).
This issue is an instance of the converse error as detailed by Aristotle.
The Bible is true and therefore without errors. (forward reasoning).
No errors in the Bible means the Bible is true. (converse reasoning)
The converse error is to think that if one can eliminate all errors in the Bible the Bible will then be true. Note that the Bible makes clams that go outside of space and time. An information argument would work. A physics argument would not work.
On the other hand, one way to determine that the underlying text is true is to find some form of authentication codes in the text. These authentication codes do not require that
everything in the Bible translations today be true. Error correcting codes are used in DNA (by the creator), in video and audio communication (by humans), etc.
16. Implications
What exactly does this show?
☐ There is a creator God outside of time and space.
☐ The Hebrews had an idea of pi (like many other civilizations) that was lost in translation.
☐ Something else.
Fault tolerant and/or error correcting codes can identify and correct unavoidable mistakes or errors in transmission. Forcing a transmission to have no errors does not in and of itself require a creator God outside of time and space (as we know it).
There can be authentication codes in a document even if there are (certain) errors of creation and/or transmission in that document.
The ratio (see below) of
106/111 is more accurate than any ratio of integers with each value up to
300 except for
233/244.
17. Email analogy
Suppose an email message (Bible) arrives that claims to be from your boss (God).
You find some spelling and grammer errers, but can still understand the message. Due to inerrancy considerations, you might reason as follows.
The boss made a mistake. I can ignore the message.
Someone must have changed the message but the original was inerrant.
Does it matter?
The message tells me about things that only the boss (God) knows. (authentication code)
Is the authentication more important than any spelling or grammar mistakes in the message?
Discuss: Why do some people spend more time arguing about spelling and grammer errers and fixing them than in actually doing what the message says to do?
[spoofing, man in the middle attack, Shannon, Hamming]
18. Lua code - one over one third pi
Here is the Lua code [#2]
19. Output - one over one third pi
The output shows the best
20 integer ratio approximations where the denominator ranges from
1 to
300.
0.31830988618379... (desired value is pi/3)
Here is the output of the Lua code.
20. Exponential constant

e(0.0) = e0.0 = 1.0000...
e(1.0) = e1.0 = 2.7182...
e(2.0) = e2.0 = 7.3890...
...
|

The exponential constant e, Euler's number, discovered by Jacob Bernoulli in 1683, is defined such that the slope (first derivative) of the function e(x) is e(x) (i.e., as a fixed-point). The value of e = e(1.0) = e1.0 is approximately 2.718281828459.
Numbers such as e are transcendental and, like irrational numbers, have no exact representation and can only be approximated.
|
21. Infinite series
Here is an infinite series (one of many) that has the value of
e, where
! is the factorial function.

For more information on the factorial function, see
Permutation: Introduction.
Transcendental numbers can be approximated by a rational number as the ratio of two integers.
Consider the transcendental numbers
e.
Consider the approximation of
1 over
e. This is done to get a ratio between
0.0 and
1.0.

22. Manual approach
A manual approach is to start trying values for numerator and denominator and see which is closest. There may be clever ways to prune the search. Here is a grid to show the best approximations for denominators ranging from 1 to 10 and numerators ranging from 0 to 10. The best approximation below and above the desired result is in light green while the others are in gray.
23. Manual grid
24. Program approach
With the use of computer programming code, is easy to find rational approximations to non-rational numbers. Note: The program is intended to be somewhat clear, but not necessarily the most efficient.
25. Lua code
Here is the Lua code [#3]
26. Output
The output shows the best
20 integer ratio approximations where the denominator ranges from
1 to
300.
0.36787944117144... (desired value)
Here is the output of the Lua code.
The smallest set of integers that gets close to
e, from this analysis, would be
25/68.
27. Euler's identity
The value of the constants
π, sometimes written as "
pi", and
e are two of the
fundamental constants in mathematics. These constants appear often in formulas in physics, engineering, etc., and are related by
Euler's identity.
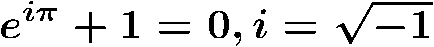
Both
π and
e are transcendental numbers that are defined by in infinite series of diminishing term values (see below for an example of each).
The term
i is the
imaginary number as the square root of
-1.
The use of
imaginary numbers allow these mathematical relationships to be applied to physical phenomena such as electricity and magnetism.
28. End of page
 The radius r of a circle is half the diameter d, so the following holds.
The radius r of a circle is half the diameter d, so the following holds.








